More Orbit Calculus
Page(s) in the works
Scripts for Orbit Determination
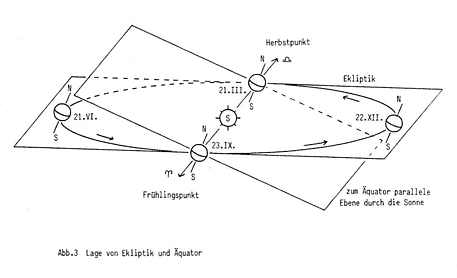
The orbit determination happens from one single observation-point of the earths surface, while the motion of the earth (with the observer) must be calculated out. The latter is not the subject of the scripts. Although the moving position of the observer is a big calculation, this is self-understanding for all observations, so that thereafter the position of the celestial body is obtained with reference to the sun in the ecliptical coordinate system. The long term fluctuations of the ecliptic and equator must be calculated out (precession and nutation), this is self-understanding and belongs automaticly to the procedure as well as the runtime of the light and the abberation in the telescope, because while ligth passes the telescope, the telescope moves with the motion of the earth. And the orbit of the celestial body is anyway determined from the attraction force of the sun unless it comes not near to a solar close planet, so that the attraction force of this planet is stronger than the one of the sun. In this case we would have the so-called 3-body problem and this is not object of the regarding here.
If the observer measures exactly the angles longitude and latitude of the celestial body at 3 positions to 3 different points of time versus the star background, which serves as a scale, the distance is invisible, but it can be, after above mentioned calculation, calculated the distance to the celestial body from the sun (this is explained in the script). The angle-velocity as well as the change of the angle-velocity delivers the information of the entire orbit of the regarded celestial body. The change of the change of the angle-velocity result from, that it is known, the orbit can only be a conus section line. And this is all described here in the scripts. The invention of the mathematic methods are a great performance of the mankind
It would be certainly possible for a single man, who knows the mathematics, to write a computer program in half a year to get the orbit of a new discovered comet per mouse-click. He can take the observation data from an observatory publication. For study of all the mathematics of orbit calculus I can recommend the book "Grundlagen der Ephemeridenrechnung" by Oliver Montenbruck
Bahnbestimmung-1980-Laplace-Stumpff-Herget-Abschrift.pdf
Bahnbestimmung-1982-Gauss-Veithen-Merton-Abschrift.pdf
Lecture.pdf
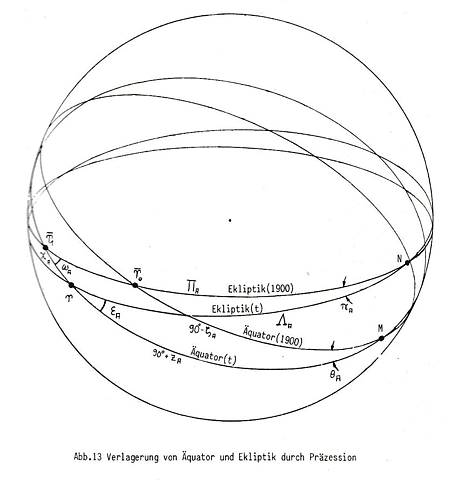
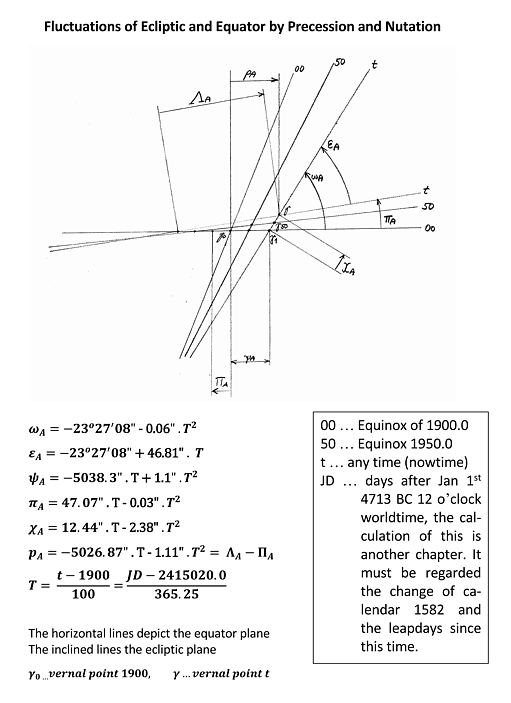
Fluctuation of Ecliptic and Equator
Calculation of Wintertime
Version of 1990
|
Coarse Concept of the Calculus of Wintertime
For getting winter-time the True Anomaly must be 90 degrees from the vernal point.
For getting the true anomaly it must be got the Excentric Anomaly and for getting this it
must be got the Normal Anomaly.
The Normal Anomaly is an angle, growing linear with the time
after the equinox and is not zero at the equinox time. But it is not exactly 360 degrees per year,
because the year is not exactly 365.25 days. This is compensated by the leap days (not perfectly exact after 1000 years),
but this is a calendar date and not a continuous time. And so the Normal Anomaly must be taken from a table
of ephemeries and substracted all multiple of 360 degrees. From this the True Anomaly can be calculated.
Now the earth orbit ellipse, with the sun in one focus is turned in the ecliptic around the sun
for approx. 101 degrees from vernal point. This is the lenght of the perihelion, the angle of the major semi axis.
This must be added to the angle of the True Anomaly and this is thereafter the position of the earth in
heliocentric ecliptical coordinates.
For getting winter-begin, it must be chosen the True Anomaly so, that it together with the
lenght of perihelion has 90 degrees after the vernal point, because that is 90 degrees in the equator plane.
The True Anomaly has than approx. -11 degrees or better 349 degrees in the year before. And thereafter the
calculation must be made backward to get the Normal Anomaly and to this you must add the Normal Anomaly of all
the years since the exinox. From there you get the Calendar Date and Time out of the procedure unterneath.
| |
Julian Date and Calendar Date
Version of 2017, Programming Language vbScript
last update Dec 18th 2019
